Category Archives: Uncategorized
Bring Back the Rigor in the Math Classroom!
Math is difficult for a lot of students. Math teachers struggle on a daily basis in how to teach math to their kids and to do so effectively. Over the last few years, I have noticed a trend in math instruction as teachers try to effectively change their pedagogy in their classroom. We have lost our focus – the focus on good math instruction. Nothing can take the place of an effective teacher who focuses their class around quality, rigorous content. There is no computer program, trend, or new class model that will ever be more effective than a teacher that knows their standards well enough to develop a rigorous, challenging lesson. We have lost sight of this as teachers across the nation are being sent to workshops and trainings on the newest way to teach math. We are spending too much of our time developing math games, fun activities, online training lessons, etc. rather than on the actual math being taught. Focusing on the math content first and adapting that to an activity is far more effective than putting the focus on doing fun activities first.
Learning should be at the forefront of every one of our decisions for our classroom. Regardless of the approach you take in delivering instruction, if your children are learning then what you are doing is successful. It shouldn’t matter the approach you take since the students are showing growth and learning. Direct instruction, it seems, has developed a negative connotation for those teachers who lead class with a direct instruction approach. John Hattie’s research states that direct instruction has a 0.6 effect size. This lands in the “high impact” interval which means that direct instruction has a high impact on student learning. If your children are learning and showing growth in a direct instruction classroom, then direct instruction works for you. As you know from my previous blog posts, I practice the flipped classroom model. My kids show growth and learn so then the flipped classroom works for me. Rather than focusing on the method of instruction, the focus is always on the learning. Regardless of what method of delivery I choose, my focus is always on the learning and content.
In addition to the method of instruction, there seems to a push to use online math programs. There are numerous programs such as IXL, Khan Academy, DeltaMath, Freckle and TenMarks that teachers can use to give students supplemental work. These programs can be great supplemental tools to enhance classroom content but they shouldn’t solely be used. Sitting a kid in front of a computer program to have them answer 5 questions in a row is not showing mastery. Again, nothing can take the place of quality, rigorous content. I have noticed a push of numerous districts forcing these programs upon classroom teachers. These programs can have all of the bells and whistles which include games, badges, cartoons, etc. but we have lost what is most important – content. Regardless of the fun stuff, how is the content? Is it rigorous? Does it help with depth of understanding of content? Recently, I learned more about one of these programs. The presenters were energetic, the platform was awesome but then I started to delve into the content. I started asking these presenters questions about where I could find the content on (insert topic here). They were unable to provide me that content. What they interpreted the standard to be wasn’t actually at all what the questions were asking and the questions didn’t align to the standards at all. They were more focused on the platform and engagement of the content rather than the content itself. At best, the content was adequate but most content wasn’t good. It was very basic and didn’t ask what kids truly needed to know to show mastery of content.
We cannot succumb our kids and classrooms for the next best new program or fad that comes along. Learning and content must always be put as a priority. Math can be made exciting with activities, games, etc., but if the quality of the math used in those activities and games are not rigorous then we are wasting our precious class time for a feel good moment with kids rather than teaching the math skills they need. We need math classrooms where students are exposed to a quality, rigorous curriculum.
Math Textbook or no Math Textbook?
I am nearing my 17th year of teaching and I’ve noticed more and more people jumping on the anti-textbook bandwagon. It’s a trend that I just don’t quite understand nor do I agree with. Why are we putting so much focus on getting rid of the use of textbooks when our focus should be on the learning? There are great teachers who teach from textbooks and great teachers who don’t. There are also ineffective teachers who teach from textbooks and ineffective teachers that don’t. The textbook isn’t what makes a great teacher great or a bad teacher bad. A textbook, like anything else we use, is just a tool.
I love teaching math and I absolutely love giving students rigorous and thoughtful problems. Problems that sometimes take 20-30 minutes each. The ones that get kids to talk to each other, to collaborate and to persevere. These problems are ones I rarely make up on my own. I have a multitude of resources I pull problems from and some of these resources are textbooks, however, a textbook will never drive my instruction. The needs of my students’ learning will always drive what happens in my class. The ability of what I do as a teacher is by far the most important aspect in what makes my students successful. A textbook doesn’t make my students successful nor does it make them unsuccessful. I know my standards, I align everything I do to those standards and most importantly I know my students. I know that what I give them for work is purposeful and when they practice these concepts, they are learning. The problems I have my students work through quite often come from a textbook. Everything I do comes from my choices as an educator who tries to do the absolute best job I can based on all of the knowledge I have learned in my career to help students love math and succeed.
I’m unsure where this anti-textbook push has come from and uncertain how the textbook itself has taken all of the blame. Quite possibly a textbook is looked at as being too traditional. We often remember our own math classes as being ones in which you would take notes from a teacher at the front of the board talking through examples as you feverishly wrote everything down in your notebook. Then you would go home and mimic those same examples done in class for homework. But why do we blame the textbook for this? Wouldn’t this be the choice of the pedagogy as a teacher? The textbook has very little to do with the success or failure of a class or student. The teacher does.
A textbook should only be a tool that is used to support a child’s learning. Using a textbook, however, should never be looked at as being a negative. It is only a tool. Just as math teachers use protractors, calculators, compasses, graph paper, a textbook is just another tool that students can use to learn. Learning should always the most important aspect of every decision made in the classroom. If using a textbook is a part of that learning, then that is wonderful! If using a textbook is not part of that learning, then that’s equally as wonderful. There are many amazing textbooks that have been published with rigorous examples for students to learn from. I have spent hours knowing my standards. I have worked tirelessly finding examples for students to practice and work through. I would be a fool to create all of my own examples when there are many great examples out there. I select every problem I give kids to further their learning based on the standards I teach. These problems are sometimes made by me, sometimes come from a textbook and sometimes come from a resource online.
Learning should always be at the forefront of everything I do. If my students are learning and achieving their goals, then it shouldn’t matter whether or not I am using a textbook. A textbook is not the most important thing in my class just as my videos are not the most important element in my flipped classroom but I do use multiple textbooks as a resource and I am not ashamed to say I do. I have found so many great problems to use that I pull from them. I have found activities, open-ended problems and numerous other resources than enhance my students learning. In the end, a great teacher will be a great teacher regardless if they use a textbook or not and an ineffective teacher will still be ineffective regardless if they use a textbook.
4 Things that Happened Since Allowing Reassessments in my Math Class
Three years ago, I started letting my students retake their math assessments. Unsure of what to expect, I have modified the process of reassessment. Currently, students must first do corrections on their original assessment. This means they will correctly complete all missed problems/concepts. Next, students will fill out a Google Form indicating to me what standards they would like to reassess on. Here is what their form looks like:
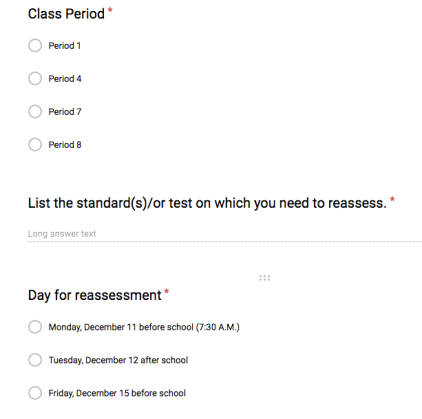
I am able to view the results so I know when students are coming into reassess so I can have their reassessment ready.

When they come in, I meet with them and discuss their mistakes and see if they have learned the material. I then give them individualized problems based on the standards they need to reassess on. I do not give them the same assessment. Once a student takes the reassessment, I score it and replace any previous scores with the current levels of mastery. For example, if a student earned a “2” on a standard and they earned a “4” on the reassessment, I replace the “2” with a “4” in the grade book.
Since implementing reassessments, there are 4 things that have happened:
- Students are learning more. Prior to allowing reassessments, I would give an assessment and students would receive a score. Students would move onto new material but would never revisit and relearn the concepts they struggled with on the assessment. Since allowing reassessments, students are now taking the time to learn the material again. They are coming to me saying, “Mr. Humphreys I need more help in understanding….” They are asking for examples. They are asking for more practice. They are initiating the conversation to learn.
- Students are taking ownership. Students are now taking the responsibility to sign up for reassessments. In my class, it is expected that students will always keep learning. Students know that if they do not “meet” or “exceed” a standard they need to relearn it. I don’t have to remind them. They take the initiative to make an appointment with me to reassess as well as to go back and do more practice to learn the concepts they struggled with. They are able to tell me, their parents and each other exactly what standards they are struggling with and the steps they are going to take to learn the material.
- Students don’t abuse the opportunity to reassess. One of the biggest assumptions is that students won’t study so they can see what’s on the original test only to do well on the reassessment. This simply does not happen. The original test and the reassessments are made so that looking at one won’t help with the other. Students are reassessing standards, not an entire test. Students would much rather do well on the first assessment as the work required to reassess is not an easy process.
- Students are excelling. Reassessing has allowed me to put learning at the forefront of everything we do. Students are learning more and, consequently, are performing better on all measures.
More than 3 years ago, I would have never allowed reassessments. I would have given every excuse as to why they would have been detrimental to my students. Today, reassessments have become a vital part of my flipped classroom. Students will always grow, always learn and always make mistakes. Reassessments have become an important part of this process. All math classrooms should allow reassessments to allow students to learn from their mistakes to continue learning.
Choice – Making it Happen with 33 Students in a Math Classroom
Last week while I scurried from my class to the hall, from the hall to the library and from the library back to my class, it happened. I realized that THIS was what I wanted my classroom to look like. I had 33 students spread out in three spaces by their own choosing all working on different things. Students choose where to sit, what to work on, how to practice and when to assess. This isn’t something that happens occasionally. It happens everyday. I often don’t take a step back to look at how awesome it looks but today I did. I was so proud of my 6th grade students and how far they have come this year. It takes weeks to get to this point and I personally always feel like I am sprinting around my room (my Fitbit would agree) but it is routine now. By letting students take ownership of their everyday environment, I ultimately have more control over my class. I have more freedom to walk around and engage with them. It is their learning, so why not let them choose how to learn. On this particular day, I had an assessment planned on the next day. Planned on this particular day was an independent study day where students would prepare for the test. Here is what my classroom liked like on this day.
Students here had already taken their assessment and were working independently on their second semester project. They have to pick any math concept they want to learn more about, learn it and make a presentation on it.
These two students were in the hall making their own problems on volume to study for the assessment.

This group of four students were working in the library (which is attached to my classroom). They worked through practice problems shared with them in Google Drive with provided answers. They picked the problems they wanted to work on and then worked collaboratively in solving them.
These students were ready to take the assessment…so they did.

These students were working on the whiteboard in my room, creating their own problems to help them study for the assessment.
This student was working on the next unit. She was done with the assessment and wanted to move onto new practice.

This student was working with a partner in next year’s content. They have already finished the entire 6th grade curriculum and wanted to move onto content for next year. Here they were working on absolute value functions.
These students chose to work individually studying for the assessment. The student on the right was doing practice problems while the student on the left was rewatching my lessons to make sure he understood the content thoroughly.

Three years ago I would never have dreamed my class could even look like this, however, by creating a classroom culture where learning is the focus through trust and choice this is how my class runs. I have allowed myself to change, give up control and redevelop how my classroom happens. Where will I be three years from now? Who knows but I am excited to keep growing with my students.
The Day I Didn’t Know a Math Standard I Taught
Two weeks ago it happened again. The dreaded moment I realized I didn’t understand the standard as well as I thought. It was demoralizing. I didn’t know the standard I was asked to teach my students. It doesn’t happen often but it does happen. I’ve contemplated making a blog post about this very topic but have always decided not to. I was leery of making myself vulnerable. Until now.
After 15 years of teaching math, I would say I know my content well. I’ve always loved math. I’ve unpacked standards, repacked and unpacked them again. For 10 years I wrote questions, based on standards, for our state test for every 7th and 8th grader in the state. The questions were quality and went through a battery of tests to make sure they were valid. They passed.
The most recent standard I thought I was teaching to my 8th graders:
CCSS.MATH.CONTENT.HSG.SRT.D.9
Derive the formula A = 1/2 ab sin(C) for the area of a triangle by drawing an auxiliary line from a vertex perpendicular to the opposite side.
The key word here was, “derive.” My students have always used the formula when finding area that involved trig ratios but never derived it. I looked at the standard and thought, “how does one derive this?” I honestly didn’t know how to derive it. I found a video online and, after quickly watching it, I quickly remembered how. The guilt then set in. How could I have not known how to derive the formula? My instruction and assessment both changed. Last week I gave my students the assessment. The question simply stated, “Derive the formula A = 1/2 ab sin(C) for the area of a triangle.” All my students demonstrated proficiency.
If there is one thing Standards Based Learning (SBL) has done, it has made me a far better teacher. I started SBL last school year. All of my assessments were now reported to standards. I made detailed rubrics that would guide students to proficiency. Prior to SBL, I had used standards in my teaching. For many years I would occasionally look at the common core standards either at a math meeting or on my own while planning. I went on with my teaching. To give myself some credit, I was teaching nearly all of the standards. I just wasn’t teaching them as in-depth as I needed to. I thought I was but when I started making rubrics, it was eye-opening. I had to make 4-point rubrics that went into detail about how students could demonstrate proficiency on each level in each standard. This alone is what has made me a far better teacher. This was my accountability. When standards drove my instruction, I became a master of the content. When standards didn’t drive instruction, I fooled myself. I taught my content first and then when I occasionally looked at a standard, I would tell myself, “Yup, I taught that.”
How could I ask my students to demonstrate proficiency on standards that I didn’t know well enough? I couldn’t.
Last year was an eye-opening year for me. I not only knew my standards, I lived my standards. Everything in my classroom was based around these standards so I had to get it right. I did. My students made more connections between concepts than ever before. I watched my students not only make connections across concepts, but also across grade levels. For example, instead of students learning Pythagorean Theorem (P.T.) in 6th grade to find missing sides of triangles they now learned that the P.T. and its converse are conditional statements as well as finding missing sides. In 8th grade they make the connection to conditional statements in geometric proofs. They then proved the Pythagorean Theorem from triangle similarity. When students learn about circles they will derive the formula of a circle all because of P.T. It all correlates. It all meshes. It makes sense. Students are aligning the concepts vertically across grade levels as well as linearly within the class.
In year two, I continually strengthen my understanding of the standards. SBL has made me keep myself accountable. I am always striving to get better. In my classroom, it’s okay to make mistakes. Failure is a part of learning. I want students to have a growth mindset and use these setbacks as ways to improve. Failure is a beginning, not an end. If I’m going to ask my students to reveal their setbacks, then I have to lead by example. Not knowing my standards in-depth was my setback but I used it to grow. I used it to improve. I will never stop learning.
The Day a Student Threw Away His Math Work
In my flipped classroom, students work on the practice in class. The practice can vary. Students will sometimes do an activity while other times students work on challenging problems that involve collaboration. The practice is always given to reinforce the concepts students learned from my videos. The practice is done in class while I walk around assessing students. Sometimes I ask questions while other times I sit back and watch them do the work.
Before my flipped classroom started 5 years ago, students would do homework. I would expect students to keep this homework in their neatly kept 3-ring math binder. I wanted students to have access to all of their homework in case they needed to pull it out to look at it. I would often do surprise checks to check how organized their binder was and, consequently, would give them a grade on it. I wanted to make sure students were learning math…by keeping all of their homework organized in their math binder. Sigh. To give myself some credit, I did the best thing I thought would work at the time. I’ve definitely come a long way in my ways to check for learning.
Fast forward to today. I no longer grade or collect any formative work. I constantly check this work daily while giving feedback, asking questions and leading students to revise their work. Students receive no score for anything other than summative work. While I no longer collect practice, the expectation is that students still are checking their work and answers with the answers I provide them. Students have answers always readily available to them. I strongly feel students need instant feedback at anytime while they are doing practice. This way students can revise in real-time not having to wait for me to come around.
Recently at the end of class I watched as an 8th grade student (we will call him Bob) finish his practice after he got a difficult problem correct. He exclaimed, “YES! Finally, I got it!” He had worked on this problem for about 15 minutes. I looked over at him with a smile. I then proceeded to watch as he got up, crumpled up his 2 pages of neatly written math practice that he had persevered in solving for an hour, and toss it in the air into the recycling bin. I was shocked. Appalled is probably a better word. How can someone who worked so hard on something throw it away!? I still thought students kept everything in a binder so they could pull it out when they study for an assessment if they needed to.
I sauntered over to Bob and asked him why in the world would he throw his work away? He responded, “Why would I want to keep it? Isn’t the purpose of the practice to help us understand the material better? I now know the material” It was a good point. Actually, it was a very good point.
I thought about what Bob said at lunch. I walked into my colleague’s office. Garnet Hillman, an awesome instructional coach, is my go to person when I have questions. I told her what happened. The replay of him crumpling up the paper and tossing it into the recycling bin replayed in my head all afternoon. Then, it hit me. Bob was right.
Why would I care if he threw the paper away? For so long, my students always did things out of compliance. Bob throwing the paper away, right before my very eyes, proved to me one thing. Bob cared more about learning than compliance. He did the practice and persevered through the work to learn. He reflected on his work throughout class through my feedback and by checking his answers. The learning happened! Once the learning happened, there was no reason to keep the practice. It wasn’t about compliance, it was about learning. There was no grade attached to the work, therefore, the primary focus of completing the work was to LEARN it, not to earn a grade.
Two years ago I stopped grading and collecting work as it was eating up so much of my valuable time. I honestly thought students would no longer do it since I wasn’t giving a grade for it. Just the opposite happened. They kept producing quality work. Fast forward to a day last month when I watched Bob throw away his work. Little did I know at the time but Bob just solidified everything I was hoping would happen. Students were now doing the work because of the learning, not because of compliance for a grade. There was no need to keep the work. The practice was used to learn the concept. Thank you Bob!
Getting Rid of Time Limits on Math Assessments
In my journey to make my assessments better, my most recent change has been to eliminate the time restrictions I have imposed on my assessments. Looking back over the last couple of years I now see that I was slowly shifting away from giving students time limits as my classroom became more student-centered.
For a little over 13 years, I gave one class period to take an assessment. At the end of class, it was typical that I would collect and grade the assessments. I expected students to be done by the end of class. I wasn’t consciously or purposely causing kids to have anxiety over my tests but it was what I’ve always done and what I thought worked. At the time, I did what I thought was best but was it best for my students’ learning?
A little over two years ago, I put a lot more emphasis in creating tests that were not only aligned to my math standards but also assessed students on in-depth learning of content. As always, I created tests that I thought students would be able to finish in a class period. However, what I found out was that as I improved the quality of questions I asked of students, the tests that I created were too long and students needed more than one day to complete them. I remember how I felt on these days. I would hand out the test and as the end of class neared, no one was turning them in. I panicked. How can they possibly take this long? How can I start the next unit tomorrow if they aren’t done with the test? The rational side of me kicked in and I remember saying to myself, “Who cares?” I collected the tests at the end of class and gave them one more day. The day went on everything was fine. I made notes to myself to make the tests shorter for the next year.
Last school year, I tweaked my assessments while also changing the way I assessed students. None of the assessments I gave last year had time limits. Some students would be finished in 30 minutes while some make take 3 days. I began to let students choose when they were ready to assess and in doing so, also gave them the choice in how long it took them to complete the assessment. What happened was remarkable. The stress that was put on students to complete the test in a certain time limit was gone. The anxiety had subsided and students spent way more time and energy in producing amazing work to show their learning rather than how fast they can do it in. I wasn’t without my doubts. There was always a part of me that thought if a student wasn’t done with a test, they could go home, look up an answer and study some more. I worried that they would use this time to cheat. What would be the point of studying for an assessment if you could just get the assessment, then go home and study what was on the test? Let’s be honest though. If my students could go home after viewing my test to look up an answer or method to only write it on the test the next day the problem isn’t with the student. The problem is with the quality of tests I am writing. If I do write a quality test and my students go home to study and prepare more after they’ve seen the test, why is this a bad thing? Don’t we want them to study? Don’t we want them to problem solve? Isn’t this what we do as adults on a daily basis? We use the resources around us to make us better at what we do.
I have given unlimited time on assessments for over a year. The quality of work has improved. Students now check their work making sure their answers are reasonable. A lot of students now use multiple ways to solve a problem. Some students make their own examples to prove or disprove items. Students are making fewer and fewer math errors that would be considered minor errors. At the end of the year, my students took a final exam that align to the high school standards. This final is identical to the final given at our local high school as my students are taking the same course in junior high. There was a time limit. I informed them of this time limit early on. I told them to not worry about the time limit and to focus on the content. Even though I told them not to worry, I was worried about it. I hoped they would have enough time. In hindsight, what did I do? I sparked the fuel of anxiety once again.
Research has shown that anxiety actually causes a brain to almost shut down when doing math. Jo Boaler, a mathematics professor at Stanford University, has done significant brain research on what anxiety does to a math brain. Take a moment to watch this video on research on the brain in relation to math. One of Jo Boaler’s four math points is, “Speed is not important.”Boosting Math is a great video highlighting four points with teaching math.
While students were taking the final, it was apparent that they wouldn’t finish with the given time limit and it wouldn’t even be close. I made the decision that knowing the content and proving to me their learning was far more important than deciding how fast they should do it in. I interrupted them and told them the time limit was gone. The sighs of relief could be heard and for the rest of the class period and a whole other class period the work students produced for their final was some of the best work I have ever seen in 15 years of teaching. Students were producing arguments, proofs, reasons, counterexamples and pages upon pages of extra work that showed their learning.
For more information on Jo Boaler, the growth mindset and her work on Inspiring all math learners check out YouCubed through Stanford University.
Math tests – Why I was failing my students and how I changed.
Why do most math tests look the same?
For 12 years I gave math tests that looked like this:

This test was created and given in 2012 to 8th grade Algebra students. I never intended to make tests that showed nothing more than doing rote memorization of skills. At the time, I honestly thought this was a great test. For 12 years I created tests where a majority of the problems were just like the problems we did in class. I then would put one or two challenging problems and the last question would be a bonus problem. It was the typical way I had always been taught and it was the way all of my tests looked when I was a student. It wasn’t a bad test. It just wasn’t enough.
I never was assessing what the kids were truly learning. Rather, I was assessing whether or not they could mimic the problems in class. Had I given my students a completely different, more challenging problem that required multiple steps and thorough understanding, they would have struggled. The bottom line.. I wasn’t assessing the standard.
In December of 2014 I remember deciding to scrap an assessment for my 7th grade students who were learning how to solve systems of equations. In my mission to give students more choice, I remember throwing out the copies of the paper test and sending them this shared document:

I asked my students to, “prove they have mastered the standard.”
My students opened this document and instantly panic set in. The students started to react:
“What do you want me to do?”
“Tell me exactly what you want”
“How long should the this be?”
“How do I get an A?”
“Where’s the test?”
It became very clear that after all of these years, I had failed my students. They weren’t concerned about the in-depth understanding of the concepts. They wanted to comply. They wanted to play the game of school they were so comfortable with. They wanted to take this test and earn the grade.
I honestly had no clue if this would work. Would my idea crash and burn? Would it take 2 days? 5 days? Did I actually teach them well enough to do what I am now asking from them? To prove understanding.
Students worked for 3 days in class on this. I gave them no direction as to what to actually do. I gave them feedback…quality feedback. One child was working through his presentation to which he said he was finished. The work he had done was superb but I looked over it and noticed he had forgotten an aspect of what it looks like when solving a system would yield an answer other than 1 or 0 solutions. I posed the question to him, “Can you have more than 1 or 0 solutions?” He looked up and said, “Wow, I can’t believe I forgot many solutions.” Back to work he went.
After 3 days, I received presentations, movies, paper tests and a plethora of explanations. It was clear to me. The work I had received was far better than any paper test I could have given. They were proud of what they turned in because it was theirs. They had ownership of the product they produced. I was shocked at the quality of work I saw.
Here are some examples:
In addition to collecting their projects, they would answer the questions I asked verbally. From that point on, I started to ask my students to prove understanding much more.
Let me state that I still believe in paper and pencil tests but the quality of questions I ask has dramatically increased. Questions that ask students to prove to me understanding and allow them choice in how they prove it. That’s the quality I want.
This year when testing students over quadratics, I still gave them a written test in which they had to solve challenging, in-depth problems that asked them to prove understanding. But that wasn’t the end. We went further than a test. I sent them this:

Off to work they went. I gave them no direction into how to determine the “best drinking fountain” except it had to involve quadratics. This is what I saw as I walked around the hallways:
In addition to the paper work and their verbal explanations, this is what my 7th graders turned in:
Then we went further. They built catapults to further than understanding of quadratics:
I now look at assessments differently. They are an opportunity to give students autonomy over how they prove to me understanding. I still give many paper and pencil tests but the questions asked always ask for them to prove or explain. I believe that if students truly understand the material, then they are able to explain the concept to someone else.
My challenge to you is to do something different. Step outside your comfort zone even if on the inside you are saying, “my kids could never do this.” On your next assessment simply write on the board, “Prove to me mastery over…” and see what happens. You might, too, be incredibly surprised.
Recap! The newest tool that’s changed my classroom.
It isn’t often I come across a new tool that is so profound and unique it changes how I do something in class. If that tool doesn’t help my students for the better and isn’t something that is easily integrated then it’s not something I’m going to use. It must serve a purpose and make things easier for me. It is even less often that I am so excited about a new tool that I want to publicize it to everyone I know to show them how phenomenal it is. Yesterday, I found that new tool and it is called, “Recap” found at letsrecap.com. Simply put, this formative assessment tool is amazing.
Simply put…it’s amazing.
So what is it? Recap is a way for students to submit a video response to a question that a teacher asks through Recap. As teacher I can pose questions in video or written format to students. I set the video time limit and the due date and I’m done. Students then use their webcam or phone to submit their response. It’s that simple.
Why do I like it so much?
*It’s free.
*It’s so easy to use. I don’t have to input all of the names of my students. I simply give them a class code to sign up and log in and bam! They are all added.
*The videos are all gathered in a single location. I am able to click, “play all” and quickly watch each one without having to continually open each video. It really takes about 5-10 minutes to watch a class set of videos. The picture below is what I see with all of my student video responses. I’ve disguised the students and their names. 
*It gives me a very quick and accurate snapshot of how well students understand the concepts. Students are able to rate themselves on how well they understand the question(s) asked. The graphic below shows what I see as a teacher. 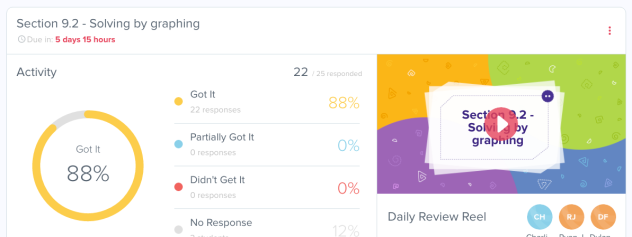
*I can share the videos with the parents of the students by either entering a parent email or sharing a unique and private weblink.
*I can give feedback to each student. By clicking the “Leave feedback” link I can quickly give each student quality feedback on their response.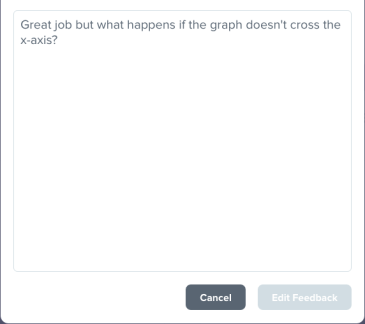
*It’s fun. Really! It is, I swear.
Here’s what I see when all students submit their responses:
So how do I use it? In my flipped classroom, I have students watch my video lectures at home. To check for understanding I submit a question to them about the concepts covered in the video. Students must explain the concept(s) to me from the video. Sometimes I will only ask, “Explain how to….” and sometimes I give a specific example. This gives me instant feedback on how well students know the concepts by how well they can explain it to me in a precise manner on video.
Thank you Recap for creating a tool that is so awesome!
7 things that happened after I implemented Standards Based Grading
It has been 8th months since I’ve fully implementing Standards Based Grading (SBG) in my math classroom and, while skeptical at first, I’ve come to realize that my students are achieving more then before. I’ve noticed quite a few changes in not only my thinking but in the overall aspects of my class. The 7 things I have noticed:
- The quality of work has increased. Make no doubt, I still give classwork. So what’s changed? I don’t grade or collect a single piece of it. I do give valuable feedback to students as I walk around the class checking on their work but I have noticed something profound. When you take grades out of the equation of classwork, the quality of work increases. I know it’s hard to believe but it follows the theory in Daniel Pink’s book on motivation, “Drive.” He states that when you make a person’s salary high enough where it no longer becomes a factor in their job, the quality of work increased because the employee never worries about doing work for pay. They do work because they are intrinsically motivated. I find the same to be true with my students. Now that grades are no longer a factor, students don’t fret over earning that grade on each piece of work. They work because they know it’s important. It’s a profound discovery I have seen first hand and one I never would have believed had I not seen it within my own classroom. Here’s an example: (Remember again that I don’t grade this or even collect it.)
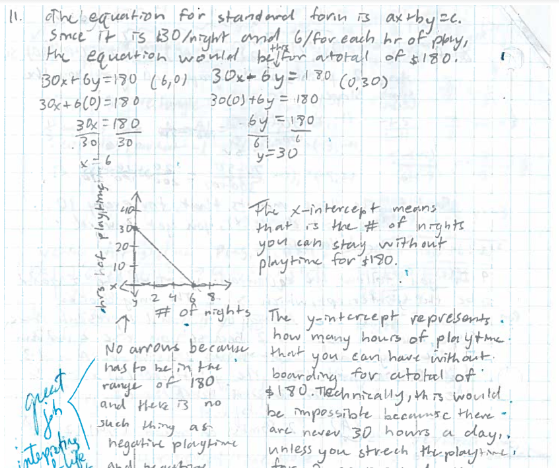
- Students have changed their language. Students no longer strive for the grade. They are never saying, “What can I do to get an, ‘A’?” I now here students tell me, “I need to reassess on the standard 7.G.4 because I need help finding the circumference of a circle.” Students know the concepts in which they need to improve upon.
- I was held accountable for knowing my standards. I am a math nerd. I know math quite well and I have always worked with standards. I thought I knew my standards well…and I did but not to the extent I needed to. When writing assessments I had to be flawless in writing questions that met the standards. It helped me to delve into my standards even farther to truly understand them.
- Grading was less subjective. With nothing factored into a grade other than content, I was no longer falsifying the grades I gave. The grade was a reflection of what the student(s) know. I grade all of my summative assessments based solely on the standards and whether or not students have mastered those standards.
- Students look at the feedback. When I put a grade at the top of the paper, students never looked at the feedback I wrote on their work as much as I had hoped. They were fixated on the grade. Once that percent and grade disappeared they started to read the feedback I gave.
- The busy work is gone. I actually feel at times like I have cheated the system that we call, “the game of school” but I no longer have hours upon hours of busy work. No longer do I have homework to grade, collect, record and pass back. It simply has disappeared. I now spend the time I used to spend grading endless amounts of work creating more meaningful lessons, videos and assessments.
- The grades now have meaning. The grades students earn are now a true reflection of what they knew. Simply put… they are now valid.














